Si $X$ es cualquier conjunto y $f:X\to X$ tiene un punto fijo (i.e.: un punto $x\in X$ tal que $f(x)=x$), entonces podemos definir en $X$ una topologia cuyos abiertos no vacios son los conjuntos que contienen a $x$. Esta topologia es conexa, pues $\{x\}$ es denso. Tambien es T_0, pues si $a,b\in X$ y $b\neq x$, entonces $\{a,x\}$ es un abierto que contiene a $a$ y no a $b$. Ademas, $f$ es continua, pues si $U$ es un abierto, $x\in U$ y por ser punto fijo de $f$, $x\in f^{-1}(U)$. Esta condicion no es necesaria ni siquiera en el caso en el que $X$ es infinito, como se ha mencionado ya en los comentarios.
Ahora voy a considerar el caso de un conjunto finito $X$, y una funcion $f:X\to X$ sin puntos fijos. Podemos definir una relacion de equivalencia en $X$ donde $x\sim y$ si y solo si existen $m,n\in\mathbb{N}$ tales que las iteraciones $f^m(x),f^n(y)$ son iguales. La afirmacion entonces es que existe una topologia $T_0$ y conexa en $X$ que hace continua a $f$ si y solo si la relacion $\sim$ no es trivial. Es decir, si y solo si existen puntos elementos $x,y\in X$ que no son equivalentes.
Antes de la demostracion, un recordatorio sobre topologias en conjuntos finitos. Dada una topologia en el conjunto finito $X$ podemos definir una relacion de orden por $x\leq y$ si $x\in\overline{\{y\}}$. Este es un orden parcial, y es equivalente a la topologia. Que $X$ sea $T_0$ significa que si $x\leq y$ y $y\leq x$ entonces $x=y$. Podemos hacer una grafica dirigida, donde los vertices son los elementos de $X$, y dibujamos una flecha de $y$ a $x$ si $x\leq y$. Entonces las componentes conexas de $X$ son justamente las componentes conexas de esta grafica. En particular, $X$ es conexo si y solo si la grafica es conexa. Por ultimo, que la funcion $f:X\to X$ sea continua es equivalente a que $f(x)\leq f(y)$ si $x\leq y$; en terminos de la grafica, esto significa que la imagen de una flecha es de nuevo una flecha.
Regresando al problema, dada la funcion $f:X\to X$, existen dos tipos de puntos: los puntos $x\in X$ para los cuales existe $m\geq 2$ tal que $f^m(x)=x$, y para los cuales no existe. La orbita bajo $f$ de un punto $x$ del primer tipo es un ciclo, y para los puntos del segundo tipo es "una trayectoria" que eventualmente cae en un ciclo. Espero que se entienda esta idea, que no es muy formal, pero creo que ayuda tenerla en mente.
Podemos hacer un "dibujo de $f$" poniendo en una fila los distintos ciclos $(a_1 a_2 \ldots a_n), (b_1 b_2 \ldots b_m) \ldots$, luego poniendo arriba de cada elemento de estos ciclos sus preimagenes, y arriba de cada elemento sus preimagenes, etcetera... anexo un dibujo MUY MAL HECHO de un ejemplo de esto.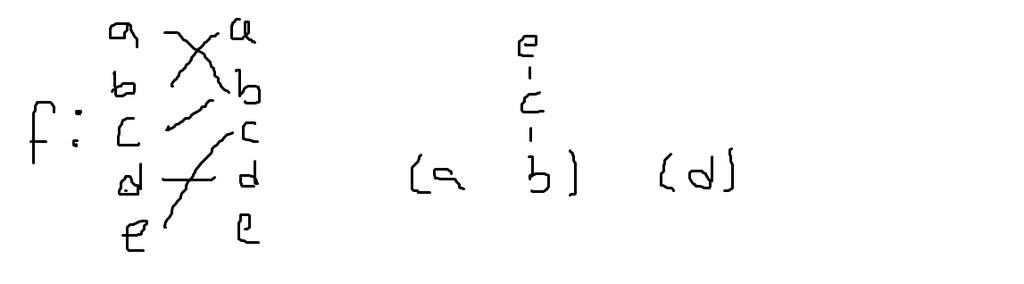
La hipotesis de que $f$ no tiene puntos fijos significa que todos los ciclos en el dibujo son de longitud al menos 2. En el dibujo feo que hice, $d$ es un punto fijo de $f$, por lo cual a la derecha aparece solo.
Ahora si con la demostracion. Primero supongamos que la relacion $\sim$ no es trivial. En terminos del dibujo, eso significa que hay al menos dos ciclos distintos. Si ordenamos los ciclos del 1 hasta $k$, definimos un orden parcial dado por $x\leq y$ si y solo si $x=y$, o bien $x$ cae en el ciclo $m$, $y$ en el ciclo $n$ y $m<n$. Como estas $m$ y $n$ no cambian al aplicar $f$, las flechas de la grafica asociada a este orden parcial van a dar de nuevo a flechas, y la topologia correspondiente hace a $f$ continua. Que la topologia es conexa y $T_0$ "es claro del dibujo".
Ahora supongamos que hay una topologia conexa y $T_0$ que hace continua a $f$, pero que la relacion $\sim$ es trivial. Llegaremos a una contradiccion. Primero consideremos los elementos $x_1,x_2,\ldots,x_k$ del unico ciclo que existe. Si $x_i\leq x_j$ es facil ver que $x_j\leq x_i$ tambien. Como $X$ es $T_0$, esto implica que $i=j$. Vamos a imaginar que pintamos a cada $x_i$ de color $i$. Si $y\in X$, pintamos a $y$ de color $i$ si $f(y)$ esta pintado de color $i+1$ (modulo $k$). Esto da una coloracion bien definida en $X$. Vamos a decir que una flecha conectando a $y$ con $x$ (que denotamos por $y\to x$) es "de color $i$ si tanto $x$ como $y$ son de color $i$. Por la manera en la que definimos la coloracion, la flecha $y \to x$ es de color $i$ si y solo si la flecha $f(y) \to f(x)$ es de color $i+1$.
Supongamos que $y\to x$ es una flecha en la grafica (no necesariamente de color $i$). Para $m$ suficientemente grande, $f^m(y)\to f^m(x)$ es una flecha en el ciclo que, por la propiedad $T_0$ implica que $f^m(y)=f^m(x)$. En particular, la flecha $f^m(y)\to f^m(x)$ es de color $i$ para algun $i$ y, por lo tanto, $y\to x$ tambien es de algun color. Lo que esto prueba es que todas las flechas son de algun color. Como hay al menos dos colores (pues $f$ no tiene puntos fijos), esto prueba que $X$ es disconexo, lo cual es una contradiccion.
Una disculpa porque la prueba sea tan confusa, larga, informal, y por no hacer un dibujo mas agradable. La pregunta me ha parecido muy interesante, por cierto.

